OEF diagonalizacija
--- Uvod ---
Ta modul vsebuje 21 vaj o diagonalizaciji endomorfizmov
oziroma kvadratnih matrik.
Iskanje lastnih vektorjev (III)
Dani sta matriki
in
, kjer matrika
pripada nekemu endomorfizmu
v urejeni bazi
, matrika
pa je obrnljiva. Čim hitreje poiščite kakšen lastni vektor endomorfizma
, ki mu v urejeni bazi
pripada matrika
. Očitni lastni vektor za
Iskanje lastnih vektorjev (IV)
Dani sta matriki
in
, kjer matrika
pripada nekemu endomorfizmu
v urejeni bazi
, matrika
pa je obrnljiva. Čim hitreje poiščite kakšen lastni vektor endomorfizma
, ki mu v urejeni bazi
pripada matrika
. Očitni lastni vektor za
Diagonalizabilnost 2x2 (dane LVr)
Dana je matrika
. Določite razsežnosti njenih lastnih podprostorov, ki ustrezajo posameznim lastnim vrednostim: | Valeur propre | dimension des espaces propres |
|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ali je matrika
diagonalizabilna?
Diagonalizabilnost 3x3 (dane LVr)
Dana je matrika
. Določite razsežnosti njenih lastnih podprostorov, ki ustrezajo posameznim lastnim vrednostim: | Valeur propre | dimension des espaces propres |
|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ali je matrika
diagonalizabilna?
Diagonalizabilnost 4x4 (dane LVr)
Dana je matrika
. Določite razsežnosti njenih lastnih podprostorov, ki ustrezajo posameznim lastnim vrednostim: | Valeur propre | dimension des espaces propres |
|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ali je matrika
diagonalizabilna?
Diagonalizabilnost 5x5 (dane LVr)
Dana je matrika
. Določite razsežnosti njenih lastnih podprostorov, ki ustrezajo posameznim lastnim vrednostim: | Valeur propre | dimension des espaces propres |
|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ali je matrika
diagonalizabilna?
Diagonalizabilnost 6x6 (dane LVr)
Dana je matrika
. Določite razsežnosti njenih lastnih podprostorov, ki ustrezajo posameznim lastnim vrednostim: | Valeur propre | dimension des espaces propres |
|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ali je matrika
diagonalizabilna?
Diagonalizacija nad R (I)
Oglejte si kompleksno matriko
in ugotovite, ali je diagonalizabilna nad poljem 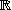 . Vnesite tudi razsežnost vsote njenih lastnih podprostorov.
. Vnesite tudi razsežnost vsote njenih lastnih podprostorov.
Diagonalizacija nad R (II)
Oglejte si kompleksno matriko
in ugotovite, ali je diagonalizabilna nad poljem 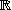 . Vnesite tudi razsežnost vsote njenih lastnih podprostorov.
. Vnesite tudi razsežnost vsote njenih lastnih podprostorov.
Iskanje lastnih vektorjev (I)
Naj bo V vektorski prostor razsežnosti in
njegov endomorfizem, ki mu v urejeni bazi
prostora V pripada matrika
. Brez računanja poiščite kakšen lastni vektor in ustrezno lastno vrednost endomorfizma.
Očitni lastni vektor: v =
Ustrezna lastna vrednost: 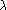 =
=
Iskanje lastnih vektorjev (II)
Naj bo V vektorski prostor razsežnosti in
njegov endomorfizem, ki mu v urejeni bazi
prostora V pripada matrika
. Brez računanja poiščite kakšen lastni vektor in ustrezno lastno vrednost endomorfizma.
Očitni lastni vektor: v =
Ustrezna lastna vrednost: 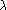 =
=
Matrike reda 2
Realna matrika
je podobna matriki oblike
(v zadnjem primeru je koeficient
neničeln).
Diagonalizabilnost 2x2 (dani LVek)
Naslednji stolpci predstavljajo lastne vektorje neke matrike A reda : Potem velja:
Diagonalizabilnost 3x3 (dani LVek)
Naslednji stolpci predstavljajo lastne vektorje neke matrike A reda : Potem velja:
Diagonalizabilnost 4x4 (dani LVek)
Naslednji stolpci predstavljajo lastne vektorje neke matrike A reda : Potem velja:
Diagonalizabilnost 5x5 (dani LVek)
Naslednji stolpci predstavljajo lastne vektorje neke matrike A reda : Potem velja:
Lastne vrednosti 1
Naj bo
končnorazsežen vektorski prostor nad poljem
in
njegov endomorfizem. Kaj lahko poveste o pravilnosti naslednje trditve:
Če je endomorfizem
, potem .
Lastne vrednosti 2
Naj bo
vektorski prostor razsežnosti nad poljem
in
njegov endomorfizem. Ali ima
vedno najmanj eno lastno vrednost iz polja
?
Lastne vrednosti 3
Naj bo
vektorski prostor nad poljem
in
njegov endomorfizem. Naj bo
in 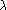 , tako da je
. Ali smemo sklepati, da je
, tako da je
. Ali smemo sklepati, da je 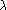 lastna vrednost endomorfizma
?
lastna vrednost endomorfizma
?
Slika in lastni vektorji 1
| Endomorfizem
prostora
ima lastna vektorja
() pri lastni vrednosti in
() pri lastni vrednosti . Določite sliko vektorja
glede na ta endomorfizem. S klikom označite krajišče iskanega vektorja. |
|
Slika in lastni vektorji 2
| Endomorfizem
prostora
ima lastna vektorja
() pri lastni vrednosti in
() pri lastni vrednosti . Določite sliko vektorja
glede na ta endomorfizem. S klikom označite krajišče iskanega vektorja. |
|
The most recent version
- Description: zbirka vaj iz diagonalizacije matrik. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, linear algebra, diagonalizacija, lastna vrednost, lastni vektor
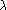 =
=
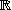 . Vnesite tudi razsežnost vsote njenih lastnih podprostorov.
. Vnesite tudi razsežnost vsote njenih lastnih podprostorov.
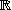 . Vnesite tudi razsežnost vsote njenih lastnih podprostorov.
. Vnesite tudi razsežnost vsote njenih lastnih podprostorov.
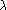 =
=
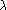 =
=
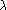 , tako da je
. Ali smemo sklepati, da je
, tako da je
. Ali smemo sklepati, da je 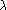 lastna vrednost endomorfizma
?
lastna vrednost endomorfizma
?