Let
be a polynomial, defined in 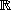 by
.
by
.
Let
be differentiable in 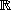 . Determine the derivative.
. Determine the derivative.
=
NB : write "sqrt(a x+b)" for
Let
be a polynomial, defined in 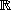 by
.
by
.
Let
be differentiable in 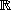 . Determine the derivative.
. Determine the derivative.
Determine the derivative of a function in 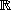 defined by
with :
defined by
with :
The functions and are differentiable in and :
In order to determine the derivative of we apply the following rule of differentiation:
The derivative function of will be :
Given the function
defined in
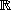 by
.
by
.
We will now determine the derivative of in a few steps :
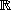 by:
by: 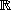 :
: en
and
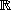 .
. | Given the plane . The curve C is the graph of the function , defined in . The line is the tangent of C in point , with coordinates ( : ). Point , with coordinates ( : ) is also on line . Determine the value of at two decimals accurate. |
xrange -, yrange -, parallel -,-,-,,1,0, 2*+1, grey parallel -,-,,-,0,1, 2*+1, grey hline 0,0,black vline 0,0,black arrow 0,0,1,0,8, black arrow 0,0,0,1,8, black text black , -0.5,-0.3,small , O text black , 1,-0.3,small , I text black , -0.5,1,small , J text blue , -+0.5 , , medium, y=f(x) linewidth 1.5 plot blue, plot green,
|
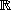 by
.
by
. Investigate this function and determine the extremum (extrema) of .
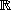 :
: Please take note that WIMS pages are interactively generated; they are not ordinary HTML files. They must be used interactively ONLINE. It is useless for you to gather them through a robot program.